Survival analysis
· If the dependent variable is time to an event then we have to undertake a completely different type of statistical analysis.
· There are a number of problems with analysis of time to event data.
· Let us take for example a case of new THR implant with a 10-year follow-up and the outcome of interest is revision.
· Some patients will have 10-year follow-up.
· Others may be recruited at the end of the study and therefore only have a 5-year follow-up.
· Some patients will be lost to follow-up.
· Other patients will die.
· Some patients will not have been revised at the end of full 10-year follow-up.
· How do we know what happened to all those THR that did not undergo revision?
· Survival analysis is a way to analyse these data.
· In a survival analysis we are interested in a clinical course duration that begins with the enrolment and ends when the patient experiences the outcome of interest (revision).
· In a survival analysis you either experience the outcome or not.
· Patients who do not experience the outcome (for reasons outlined above) are termed “censored.”
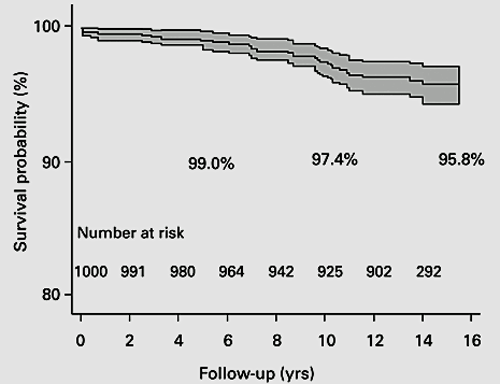
Figure 23 Kaplan-Meier survival analysis of Birmingham Hip resurfacing implantKaplan-Meier survival analysis of Birmingham Hip resurfacing implant.Graph shows the survival probability with 95% CI CI gets wider as the numbers at risk get smaller..Note that authors indicated how many participants were left at each stage following censoring.From Daniel et al. B Joint J 2014; 96-B: 1298-1306.
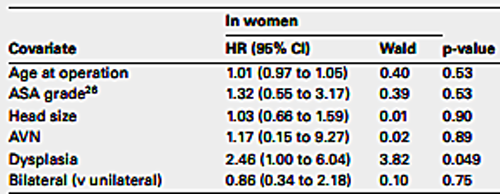
Figure 24. Cox regression analysis.The authors were interested to investigate the impact of several covariates on implant survival. Therefore they performed Cox regression analysis. In this chart which we can see that a diagnosis of dysplasia in women was the only statistically significant covariate increasing the risk of revision.
· Therefore in a survival analysis it is important to show how many participants were censored.
· In a survival analysis as the number of participants decreases with time the statistical estimate becomes less and less certain.
· This is evident by the widening of confidence intervals from left to right.
· Therefore one should be cautious about interpreting results on the far right of the curve especially when it is not known what was the population at risk (numbers left in the study).
· It is also important to realise that in survival analysis what is calculated is the known survival time.
· As it is not possible to know what will happen to censored patients as soon as a patient is censored the curve becomes an estimate.
· Although authors like to estimate longest follow-up and the survival rate thereof it is best to look at the minimum follow-up time as the survival rate at this time is likely to be the most accurate.
· An important assumption in survival analysis is that the probability of a participant being censored is not related to the probability of that participant experiencing the outcome of interest.
An example (Figure 25)
· One thousand patients having a THR are followed up for 10 years.
· Person –years at risk is 1000x10=10,000
· If there were 100 revisions over 10 years the revision rate would be 100/10000= 1 per 100 person-years
· From National joint Registry,cumulative risk of revision for cemented primary knee replacement. It shows that of the implants used the posterior stabilised, mobile bearing TKR consistently had the highest risk of revision(figure 25).
· Dataset indicates the persons at risk at each stage due to censoring.
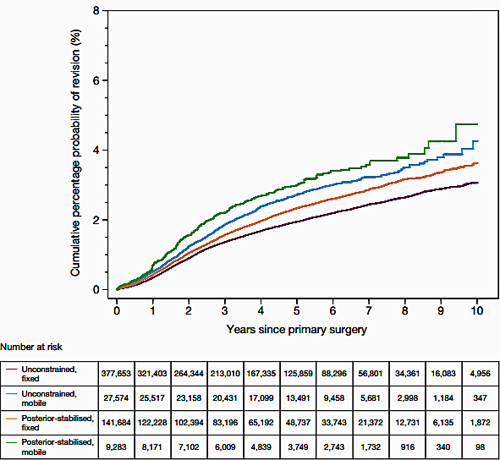
Figure 25. Survival analysis.Person –years at risk is 1000x10=10,000.If there were 100 revisions over 10 years the revision rate would be 100/10000= 1 per 100 person-years
· In other words if patients drop out in large numbers from the trial because they are unhappy with the new THR implant then survival analysis will not be valid.
· A benefit of survival analysis is that every participant contributes data to the study however short a period they remain in it.
· The dependent variable in a survival analysis is known as a hazard.
· If we consider revision as our outcome of interest then hazard is the risk of being revised at a point in time, having survived up to then without being revised.
· When using survival analysis one cannot calculate the mean survival time as it does not take into account differing follow-up times.
· One uses cumulative survival time (for example 10-year survival probability).
· Log rank test is performed to compare the survival curves of two or more variables.
· We use the Cox regression model to identify the effect of covariates on survival.
Worked out example of cumulative survival
· Let us assume we begin a trial of a new THR with 100 participants.
· At the end of year 1 there is one revision.
· At the end of year 2 there are two revisions.
· What is the probability of survival beyond year 2?
· Survival year 0 = 100
· Year 1 = 99/100
· Year 2 = 97/99
· Cumulative survival at year 0 is 100/100 = 1
· So the probability of survival up to year 1 is 1
· The probability of survival past year 1 is 99/100 = 0.99
· Cumulative probability of survival to a point is calculated by multiplying the survival rates up to that point.
· So the probability of survival beyond year 2 = 1 ´ 0.99 ´ 0.979 = 0.969
· Both the log rank test and Cox regression model assume that the hazard ratio between the groups is constant over time, if this is not satisfied then the analysis is again invalid.
· This is known as the proportional hazards assumption.
· An example is to consider that if an implant has twice the risk of revision at year 1 it is assumed that the risk of revision is roughly the same throughout the time period.
· This can be checked from the visual inspection of the plots but formal tests are also available.